Evaluación de algebra lineal

Pregunta 1

Finalizado

Puntúa 1,00 sobre 1,00

Marcar pregunta

Enunciado de la pregunta

Contexto: Este tipo de preguntas consta de dos proposiciones así: una Afirmación y una Razón, unidas por la palabra PORQUE. Usted debe examinar la veracidad de cada proposición y la relación teórica que las une.

Enunciado: Dados los vectores u, v, w en la operación de adición

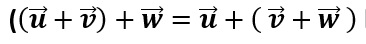
el resultado de la suma no se altera al cambiar las posiciones de los vectores PORQUE cumplen con la ley asociativa de la suma de vectores.

Seleccione una:

a. La afirmación es VERDADERA, pero la razón es una proposición FALSA.

b. La afirmación y la razón son VERDADERAS, pero la razón NO es una explicación CORRECTA de la afirmación.

c. La afirmación y la razón son VERDADERAS y la razón es una explicación CORRECTA de la afirmación.

d. La afirmación es FALSA, pero la razón es una proposición VERDADERA.

Pregunta 2

Finalizado

Puntúa 1,00 sobre 1,00

Marcar pregunta

Enunciado de la pregunta

Contexto: Este tipo de pregunta se desarrolla en torno a un (1) enunciado y cuatro (4) opciones de respuesta (A, B, C, D). Solo una (1) de estas opciones responde correctamente a la pregunta:

Enunciado: Hallar la inversa de la matriz A:

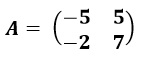
Seleccione una:

a. A^-1 = -1/7 3/5
         -7/5 5/7

b. A^-1 = -7/25 1/5
         -2/25 1/5

c. A^-1 = -7/5 7/5
         -5/7 5/7

d. A^-1= -5/7 7/5
        -7/5 5/7

Pregunta 3

Finalizado

Puntúa 1,00 sobre 1,00

Marcar pregunta

Enunciado de la pregunta

La solución del siguiente sistema lineal es:

Seleccione una:

a. 

b. 

c. 

d. 

Pregunta 4

Finalizado

Puntúa 1,00 sobre 1,00

Marcar pregunta

Enunciado de la pregunta

El siguiente sistema lineal esta en forma:

Seleccione una:

a. Ninguna de las opciones es la correcta

b. Triangular superior

c. Matricial

d. De matriz de coeficientes

Pregunta 5

Finalizado

Puntúa 0,00 sobre 1,00

Marcar pregunta

Enunciado de la pregunta

El método de la matriz inversa consiste en:

Seleccione una:

a. Ninguna de las opciones es correcta

b. Escribir su matriz ampliada y aplicar operaciones elementales para transformar la parte correspondiente a la matriz A en su forma escalonada. Desúes se escribe el sistema lineal resultante y por medio de sustituciones hacia atrás, se halla la solución del mismo.

c. Escribir su matriz ampliada y aplicar operaciones elementales para transformar la parte correspondiente a la matriz A en su forma escalonada reducida.  Despues se vuelve a escribir el sistema lineal.

d. Partiendo del sistema AX= b, podemos multiplicar a izquierda por la inversa de A, con lo que nos queda:

Pregunta 6

Finalizado

Puntúa 0,00 sobre 1,00

Marcar pregunta

Enunciado de la pregunta

La representación del vector

V = 1, ángulo = 45°,

en forma rectangular es:

Seleccione una:

a. (2.43, 1.7)

b. (1.73, 1)

c. (0.7, 0.7)

d. Ninguna de las opciones es correcta

Pregunta 7

Finalizado

Puntúa 0,00 sobre 1,00

Marcar pregunta

Enunciado de la pregunta

El método de Gauss- Jordan para resolver sistemas lineales consiste en:

Seleccione una:

a. Ninguna de las opciones es correcta

b. Partiendo del sistema AX= b, podemos multiplicar a izquierda por la inversa de A, con lo que nos queda:

c. Escribir su matriz ampliada y aplicar operaciones elementales para transformar la parte correspondiente a la matriz A en su forma escalonada. Desúes se escribe el sistema lineal resultante y por medio de sustituciones hacia atrás, se halla la solución del mismo.

d. Escribir su matriz ampliada y aplicar operaciones elementales para transformar la parte correspondiente a la matriz A en su forma escalonada reducida.  Despues se vuelve a escribir el sistema lineal.

Pregunta 8

Finalizado

Puntúa 1,00 sobre 1,00

Marcar pregunta

Enunciado de la pregunta

Dados los vectores U = 2, ángulo = 30° y V = 1, ángulo 45°, la operación U+V es igual a:

Seleccione una:

a. (0.7, 0.7)

b. Ninguna de las opciones es correcta

c. (1.73, 1)

d. (2.43, 1.7)

Pregunta 9

Finalizado

Puntúa 0,00 sobre 1,00

Marcar pregunta

Enunciado de la pregunta

La magnitud del vector W = (2/raiz de 13, -3/raiz de 13) es:

Seleccione una:

a. 1

b. 5/13

c. Ninguna de las opciones es correcta

d. -1/13

Pregunta 10

Finalizado

Puntúa 1,00 sobre 1,00

Marcar pregunta

Enunciado de la pregunta

El resultado de multiplicar el vector U = (1, 2) por el escalar -2 es:

Seleccione una:

a. Ninguna de las opciones es correcta

b. (-1, 0)

c. (2, 4)

d. (-2, 4)